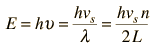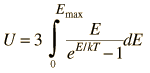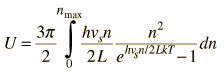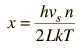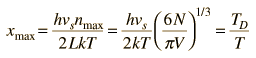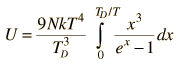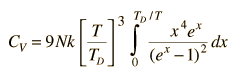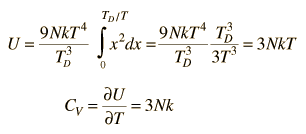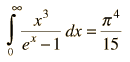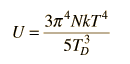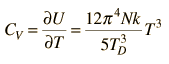What is a Phonon?

Considering the regular lattice of atoms in a uniform solid material, you would expect there to be energy associated with the vibrations of these atoms. But they are tied together with bonds, so they can't vibrate independently. The vibrations take the form of collective modes which propagate through the material. Such propagating lattice vibrations can be considered to be sound waves, and their propagation speed is the speed of sound in the material.

The vibrational energies of molecules, e.g., a diatomic molecule, are quantized and treated as quantum harmonic oscillators. Quantum harmonic oscillators have equally spaced energy levels with separation ΔE = hυ. So the oscillators can accept or lose energy only in discrete units of energy hυ.

The evidence on the behavior of vibrational energy in periodic solids is that the collective vibrational modes can accept energy only in discrete amounts, and these quanta of energy have been labeled "phonons". Like the photons of electromagnetic energy, they obey Bose-Einstein statistics.

Considering a solid to be a periodic array of mass points, there are constraints on both the minimum and maximum wavelength associated with a vibrational mode.

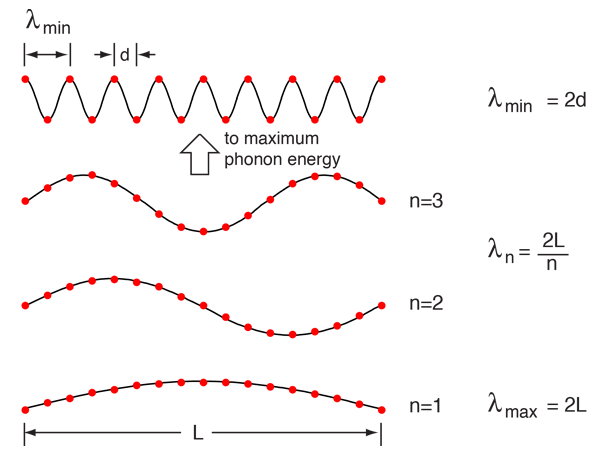
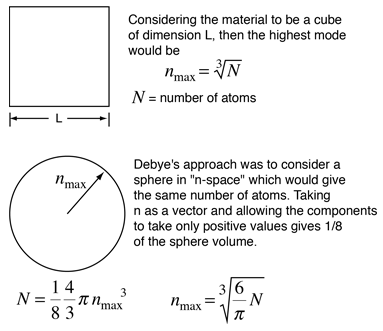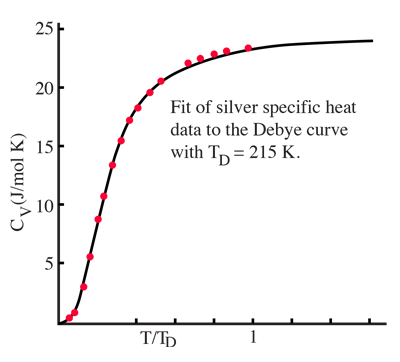
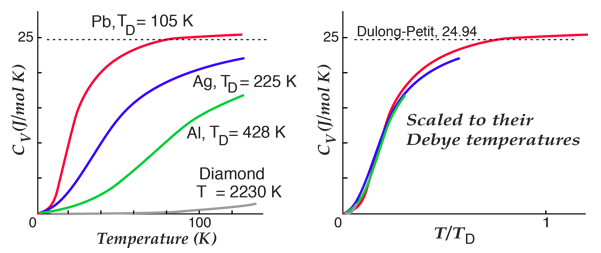
By associating a phonon energy 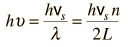with the modes and summing over the modes, Debye was able to find an expression for the energy as a function of temperature and derive an expression for the specific heat of the solid. In this expression, vs is the speed of sound in the solid.

Debye Specific Heat

By associating a phonon energy

with the vibrational modes of a solid, where v_s is the speed of sound in the solid, Debye approached the subject of the specific heat of solids. Treating them with Einstein-Bose statistics, the total energy in the lattice vibrations is of the form

This can be expressed in terms of the phonon modes by expressing the integral in terms of the mode number n.

Here the factor 3p/2 comes from three considerations. First, there are 3 modes associated with each mode number n: one longitudinal mode and two transverse modes. Then you get a factor of 4p² from integrating over the angular coordinates, treating the mode number n as the radius vector. Finally you constrain the integral to the quadrant in which all the components of n are positive, giving a factor of 1/8: the product of those is 3p/2.

The usual form of the integral is obtained by making the substitution

and the limit on the integral in terms of x is obtained from

where the constant T_D is here introduced. It is called the Debye temperature and is a constant associated with the highest allowed mode of vibration.

When all the constants are put in, the integral takes the form

The Debye specific heat expression is the derivative of this expression with respect to T. The integral cannot be evaluated in closed form, but numerical evaluation of the integral shows reasonably good agreement with the observed specific heats of solids for the full range of temperatures, approaching the Dulong-Petit Law at high temperatures and the characteristic T³ behavior at very low temperatures.

The specific heat expression which arises from Debye theory can be obtained by taking the derivative of the energy expression above.

This expression may be evaluated numerically for a given temperature by computer routines.

The data for silver shown at left is from Meyers. It shows that the specific heat fits the Debye model at both low and high temperatures.

Since the Debye specific heat expression can be evaluated as a function of temperature and gives a theoretical curve which has a specific form as a funtion of T/T_D, the specific heats of different substances should overlap if plotted as a function of this ratio. At left below, the specific heats of four substances are plotted as a function of temperature and they look very different. But if they are scaled to T/T_D, they look very similar and are very close to the Debye theory.

High and Low Temperature Limits
Debye Specific Heat

The energy expression from the Debye theory of specific heat is of the form

where TD = Debye temperature.

Even though this integral cannot be evaluated in closed form, the low and high temperature limits can be assessed.

For the high temperature case where T>>T_D, the value of x is very small throughtout the range of the integral. This justifies using the approximation to the exponential from the exponential series,
e^x = 1 + x. This reduces the energy expression to

which is the Dulong-Petit result from classical thermodynamics.

For low temperatures where T<< T_D, the exponential in the denominator becomes very large before reaching the limit, implying that the integrand is very small near the upper limit. This makes it plausible to approximate the integral by increasing the limit to infinity to make use of the standard integral

Then energy is then

and the specific heat is

This T³ dependence of the specific heat at very low temperatures agrees with experiment for nonmetals. For metals the electron specific heat becomes significant at low temperatures and is combined with the above lattice specific heat in the Einstein-Debye specific heat.