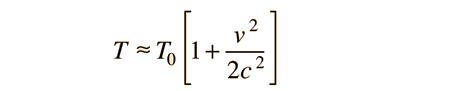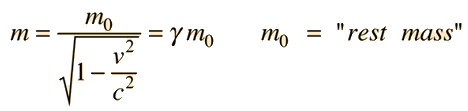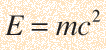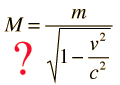"Relativistic Mass"
The increase in "effective mass" with speed is given by the expression
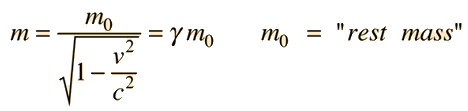
It follows from the Lorentz transformation when collisions are described from a fixed and moving reference frame, where it arises as a result of conservation of momentum. You can also approach it from the relativistic energy expression
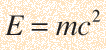
where the effective mass is given by the energy divided by c2. This suggests that this "m" is really about the energy, and that the real mass is the rest mass m0.
The increase in relativistic "effective mass" is associated with speed of light c the speed limit of the universe. This increased effective mass is evident in cyclotrons and other
accelerators where the speed approaches c. Exploring the calculation above will show that you have to reach 14% of the speed of light, or about 42 million m/s before you change the effective mass by 1%.
This language about "effective mass" is included here because it has long been used in elementary textbooks to describe the increase in energy with velocity, and it has a certain appeal for the description of relativistic effects such as the Cambridge example. But you won't find it in modern physics textbooks. One comment from a classic work on relativity is
"Ouch! The concept of 'relativistic mass' is subject to misunderstanding. That's why we don't use it. First, it applies the name mass - belonging to the magnitude of a 4- vector - to a very different concept, the time component of a 4-vector. Second, it makes increase of energy of an object with velocity or momentum appear to be connected with some change in internal structure of the object. In reality, the increase of energy with velocity originates not in the object but in the geometric properties of space-time itself." (Taylor and Wheeler in Spacetime Physics)
|