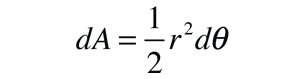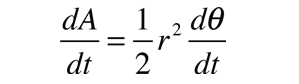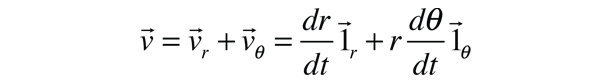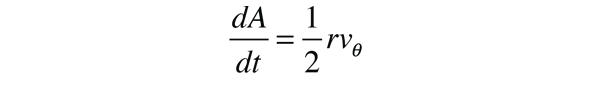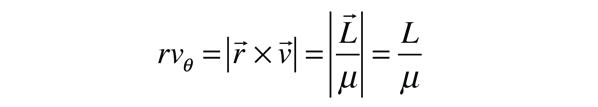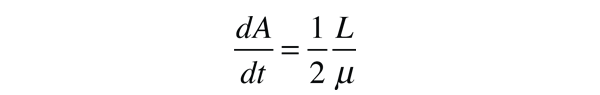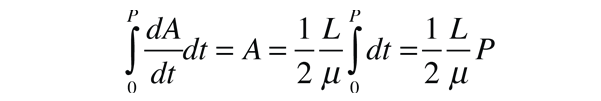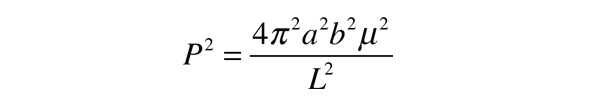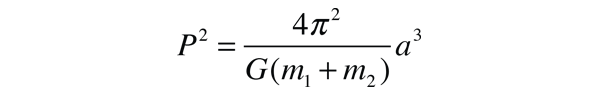Developing Kepler's Law of Orbits
Law of Orbits: two masses orbiting each other in bound orbits under the influence of the law of gravity will follow elliptical orbits about the center of mass of the two-body system.
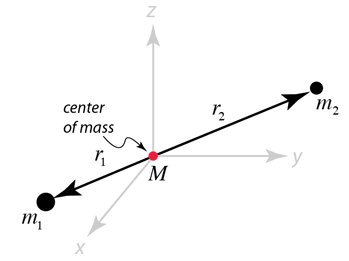 | The motion of a binary system can be described relative to the center of mass of the system. The vector distance between the two masses is 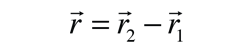 and the motion of one of the masses relative to the other uses the concept of reduced mass: 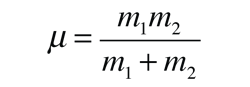 |
The individual vector coordinates of the masses can be expressed in terms of the reduced mass:

Kepler's Laws depend upon the principle of conservation of angular momentum, and since these are inherently vector quantities, the angular momentum is expressed in terms of vector products. The angular momentum of the two body system can be expressed in terms of their relative velocity and the reduced mass of the system. Starting with the individual angular momenta, the angular momentum of the system L can be expressed as follows:
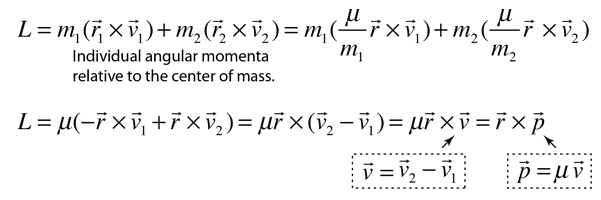
This provides the necessary framework for showing that angular momentum is conserved for an orbiting planet or a member of a binary star system. This is done by showing that the derivative of the angular momentum is zero for the case where the force of attraction acts along the line between the two bodies. This requires the expression for the derivative of a product of functions. Using the expression for angular momentum L obtained above:
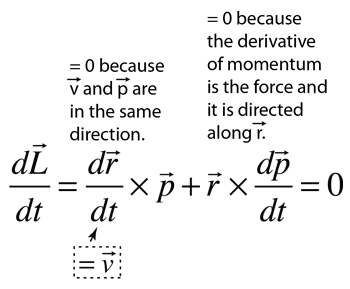 | This establishes the fact that the angular momentum L is conserved for any system of two orbiting masses acted upon by a central force. The conservation of angular momentum leads to both Kepler's Law of Orbits and Law of Areas. |
The orbit of one of the masses in a binary system can be described as the motion of the reduced mass around a point at relative distance r where the total mass is placed. The magnitude of r is the same as the relative distance r in the development above. | 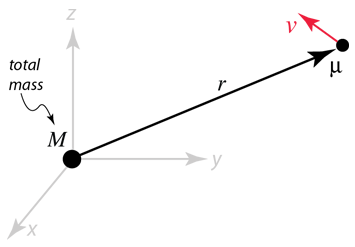 |
The determination that the motion of both masses in a bound binary system execute elliptical orbits about a focus point at the center of mass of the system requires the analysis of the force and angular momentum of the system. The angular momentum L of the system can be expressed as
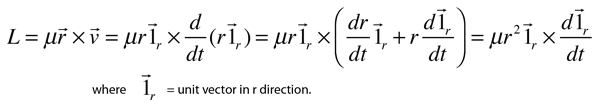
In this expression, the unit vectors in the r direction have been introduced because both the magnitude of r and its direction can change. Note that one term drops out of the vector product expression because it contains the vector product of the unit vector and itself and is therefore zero.
The acceleration of the reduced mass is given by
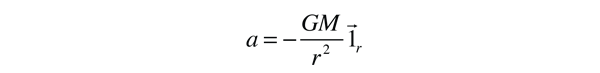
where M is the total mass of the system. As a strategy for obtaining an expression for r, the following evaluation is made:
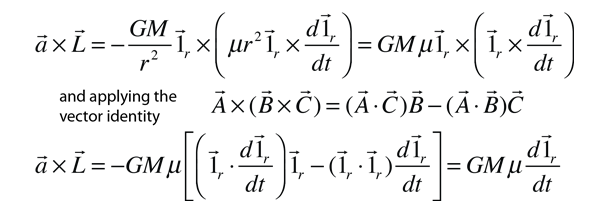
where the facts that the scalar product of two unit vectors is equal to 1 and the scalar product of the unit vector and its derivative is equal to 0 are used in addition to the vector identity.
Continuing a strategy directed toward finding an expression for radius vector r in terms of the angular momentum, the above expression is modified so that it is an equality of two derivatives. The rule for differentiation of a product is used along with the fact that dL/dt=0 (conservation of angular momentum).
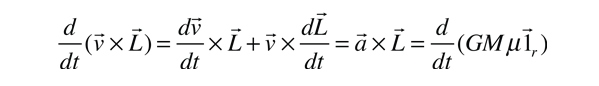
Now integrating the two differential quantities gives
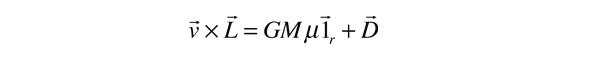
where we can argue that the vector constant of integration D must be in the plane of the orbit since the other two quantities lie in that plane. To introduce the radius vector r into this expression the following procedure with a vector identity is followed.
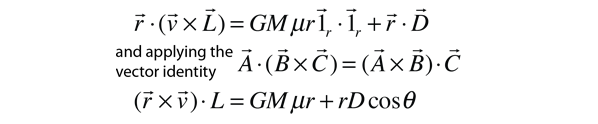
Using the final expression for angular momentum L from above, this can be put in the form
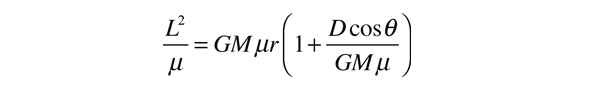
The final step in showing that this is the expression for a conic section orbit is to define e=D/GMμ so that the radius r becomes

This form for the equation of a conic section expresses it in terms of the angular momentum L, the eccentricity e, and the angle θ measured from the perihelion. For e<1 this is the form of an ellipse and can be expressed in terms of the semimajor axis a.
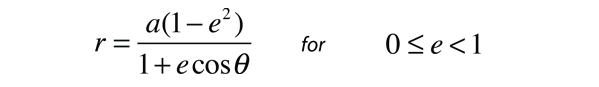
Setting these two expressions equal to each other gives an expression for the angular momentum L

 | For a bound binary orbit, each object will follow an elliptical orbit about the center of mass of the system. The center of mass will be at one focus of each ellipse. |
Gravity concepts
Orbit concepts
Carroll & Ostlie
Sec 2.3
| HyperPhysics***** Mechanics | R Nave |