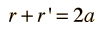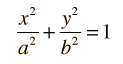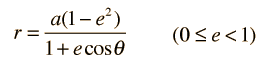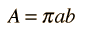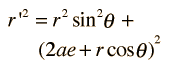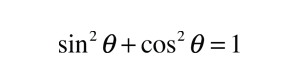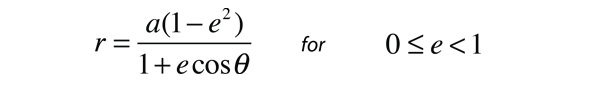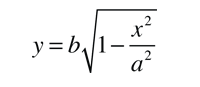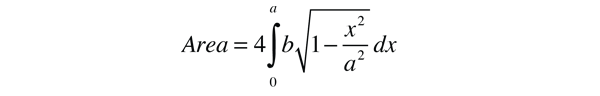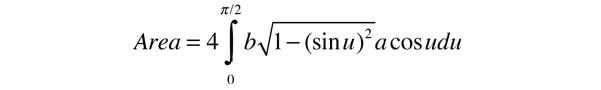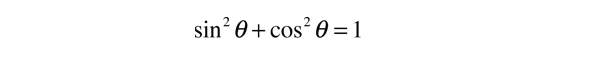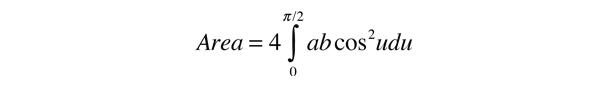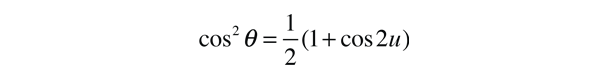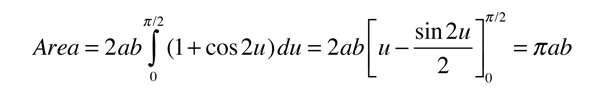Ellipses and Elliptic Orbits

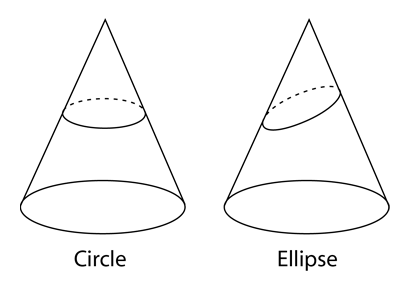An ellipse is defined as the set of points that satisfies the equation

In cartesian coordinates with the x-axis horizontal, the ellipse equation is

The ellipse may be seen to be a conic section, a curve obtained by slicing a circular cone. A slice perpendicular to the axis gives the special case of a circle.

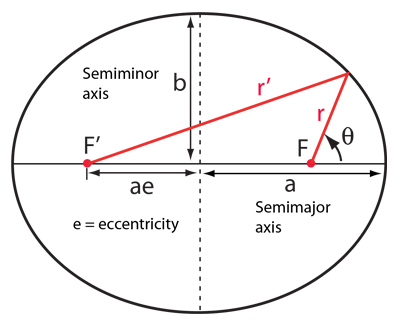
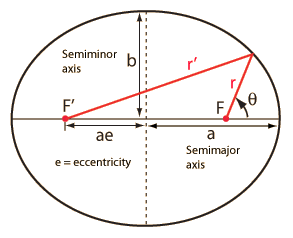
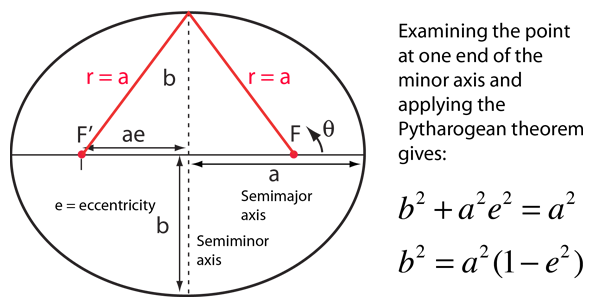
For the description of an elliptic orbit, it is convenient to express the orbital position in polar coordinates, using the angle θ:

Show
This form makes it convenient to determine the aphelion and perihelion of an elliptic orbit. The area of an ellipse is given by
Show

Each of the conic sections can be described in terms of a semimajor axis a and an eccentricity e. Representative values for these parameters are shown along with the types of orbits which are associated with them.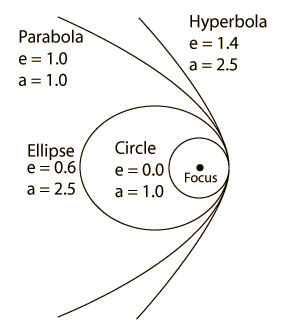

Index
 
HyperPhysics*****HyperMath*****GeometryR Nave
 Go Back





Polar Form of Ellipse

From the diagram at left, using the Pythagorean theorem to express r' in terms of r:

Using the trigonometric identity
this reduces to

Using the equation for an ellipse, an expression for r can be obtained

This form is useful in the application of Kepler's Law of Orbits for binary orbits under the influence of gravity.

Index

Orbit concepts

Carroll & Ostlie
Sec 2.1
 
HyperPhysics*****HyperMath*****GeometryR Nave
 Go Back





Area of Ellipse

Using the equation for an ellipse

the height y can be expressed as
and integrated over a quarter of the ellipse to get the area:
This kind of integral may be evaluated by using trigonometric substitution

This gives the area integral

Using the trigonometric identity
the integral becomes
Then using the trigonometric identity
this gives
Index

Orbit concepts

Carroll & Ostlie
Sec 2.1
 
HyperPhysics*****HyperMath*****GeometryR Nave
 Go Back