Motion in a Vertical Circle
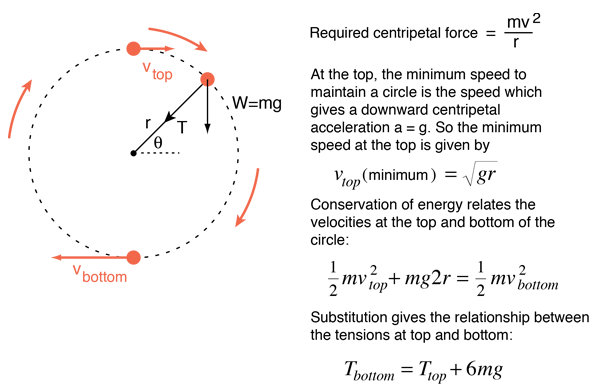
The motion of a mass on a string in a vertical circle includes a number of mechanical concepts. It must satisfy the constraints of centripetal force to remain in a circle, and must satisfy the demands of conservation of energy as gravitational potential energy is converted to kinetic energy when the mass moves downward. The velocity must increase as the mass moves downward from the top of the circle, subject to the constraints stated.
Rotational motion
| HyperPhysics***** Mechanics | R Nave |