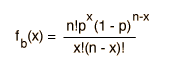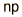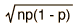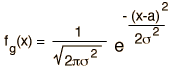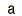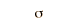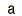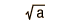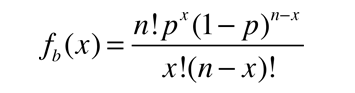Comparison of Distribution Functions

Distribution	Functional Form	Mean	Standard Deviation
Binomial
Gaussian
Poisson

Binomial Distribution Function

Distribution	Functional Form	Mean	Standard Deviation
Binomial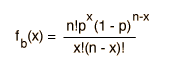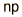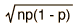

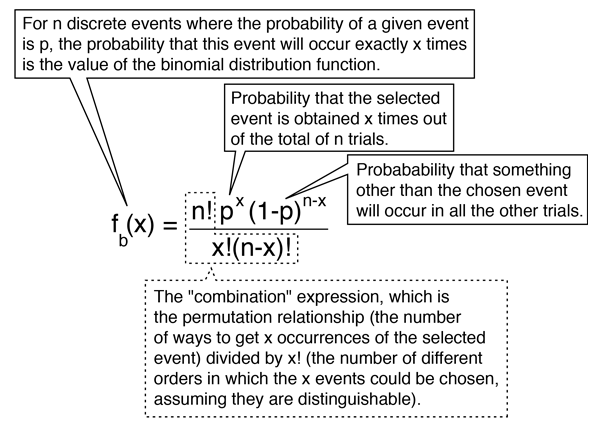
The binomial distribution function specifies the number of times (x) that an event occurs in n independent trials where p is the probability of the event occurring in a single trial. It is an exact probability distribution for any number of discrete trials. If n is very large, it may be treated as a continuous function. This yields the Gaussian distribution. If the probability p is so small that the function has significant value only for very small x, then the function can be approximated by the Poisson distribution.

With the parameters as defined above, the conditions for validity of the binomial distribution are

• each trial can result in one of two possible outcomes, which could be characterized as "success" or "failure".
• the probability of "success", p, is constant from trial to trial.
• the trials are independent.

Comments About the Binomial Distribution Function

When you examine the form of the binomial distribution function:

it is a rather formidable collection of symbols and factorials. These terms arise from an examination of the probability of discrete events. Perhaps the following summary will be helpful: