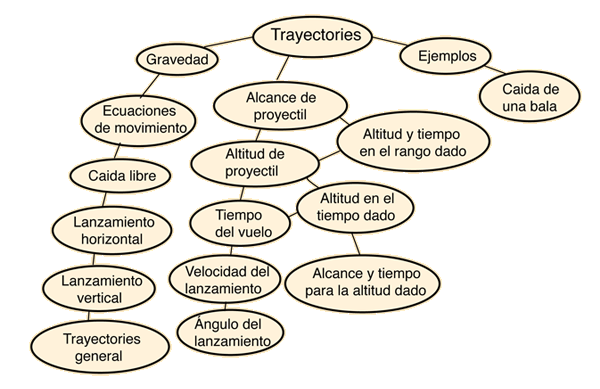
Conceptos de Movimiento
| HyperPhysics*****Mecánica | M Olmo R Nave |

|
Indice Conceptos de Movimiento | ||
|
Atrás |
|
Note que puede entrar una distancia (altura) y hacer clic fuera de la casilla, para calcular el tiempo de caida y la velocidad de impacto, en ausencia de fricción de aire. Pero el cálculo asume que la aceleración de la gravedad en la superficie es g = 9.8 m/s2, de modo que si la altura es suficientemente grande para cambiar significtivamente la gravedad, los resultados serán incorrectos.
|
Indice Conceptos sobre Trayectorias | |||
|
Atrás |
| Indice Conceptos sobre Trayectorias | |||
|
Atrás |
|
Indice Conceptos sobre Trayectorias Cálculo | ||
|
Atrás |
Lanzamiento Horizontal
| Indice Conceptos sobre Trayectorias | ||
|
Atrás |
Trayectoria Balística GeneralEl movimiento de un objeto bajo la influencia de la gravedad está determinado totalmente por la aceleración de la gravedad, la velocidad de lanzamiento y el ángulo de lanzamiento, suponiendo que la fricción del aire es insignificante. Se pueden separar los movimientos horizontal y vertical y describirlo por las ecuaciones del movimiento general para aceleración constante. En las ecuaciones se usan las componentes del vector de la velocidad inicial. El diagrama muestra trayectorias con la misma velocidad de lanzamiento, pero diferentes ángulos de lanzamiento. Note que las trayectorias de 60 y 30 grados, tiene el mismo rango, igual que lo tienen cualquier par de lanzamientos con ángulos complementarios. El lanzamiento de 45 grados, da la máxima distancia horizontal (rango máximo).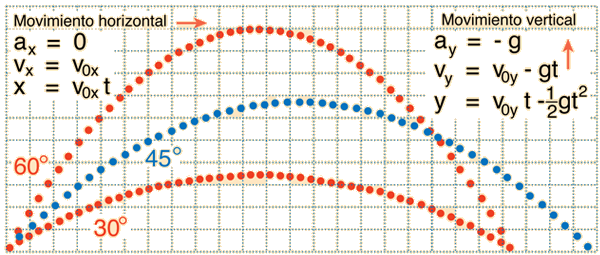
|
Indice Conceptos sobre Trayectorias Cálculo | ||
|
Atrás |
| Indice Conceptos sobre Trayectorias | |||
|
Atrás |
|
Indice Conceptos sobre Trayectorias | ||
|
Atrás |
|
Indice Conceptos sobre Trayectorias | ||
|
Atrás |
|
Indice Conceptos sobre Trayectorias | ||
|
Atrás |
| Indice Conceptos sobre Trayectorias | |||
|
Atrás |
¿Pasará la valla?La ecuaciones básicas del movimiento se pueden resolver simultáneamente para expresar y en términos de x. |
Indice Conceptos sobre Trayectorias | ||
|
Atrás |
¿Donde Aterrizará?Las ecuaciones básicas del movimiento, da las componentes x e y en función del tiempo. La solución de la distancia horizontal en términos de la altura y es util, para calcular rangos en situaciones donde el punto de lanzamiento no está al mismo nivel que el punto de aterrizaje.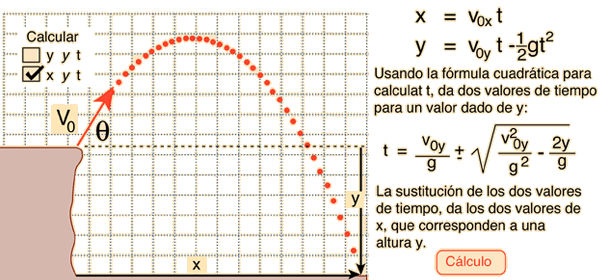
|
Indice Conceptos sobre Trayectorias | ||
|
Atrás |
¿Donde Aterrizará?Las ecuaciones básicas del movimiento, da las componentes x e y en función del tiempo. La solución de la distancia horizontal en términos de la altura y es util, para calcular rangos en situaciones donde el punto de lanzamiento no está al mismo nivel que el punto de aterrizaje. |
Indice Conceptos sobre Trayectorias | ||
|
Atrás |
Velocidad de LanzamientoSi se conoce el ángulo de lanzamiento, se puede calcular la velocidad de lanzamiento desde el rango (distancia horizontal). Tambien se puede calcular si se conocen la altura máxima y el rango, porque se puede determinar el ángulo. |
Indice Conceptos sobre Trayectorias | ||
|
Atrás |
Velocidad de lanzamientoSi se conoce el ángulo de lanzamiento, se puede calcular desde el rango la velocidad de un proyectil. También se puede calcular si se conocen la altura máxima y el rango, puesto que el ángulo se puede determinar. |
Indice Conceptos sobre Trayectorias | ||
|
Atrás |
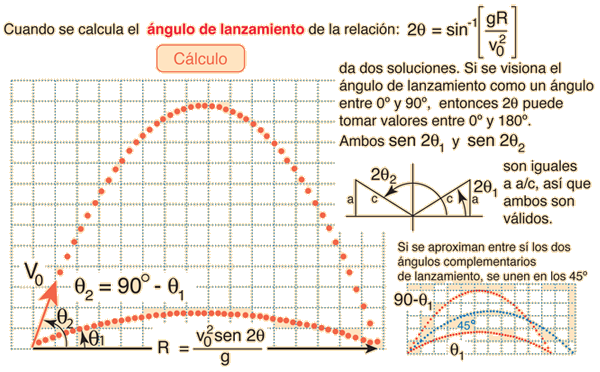
Ángulo de LanzamientoLas variaciones del ángulo de lanzamiento de un proyectil, cambiará el rango. Si se conoce la velocidad de lanzamiento, se puede calcular el ángulo de lanzamiento requerido para un rango deseado., a partir de las ecuaciones del movimiento. |
Indice Conceptos sobre Trayectorias | ||
|
Atrás |
|
Indice Conceptos sobre Trayectorias | ||
|
Atrás |