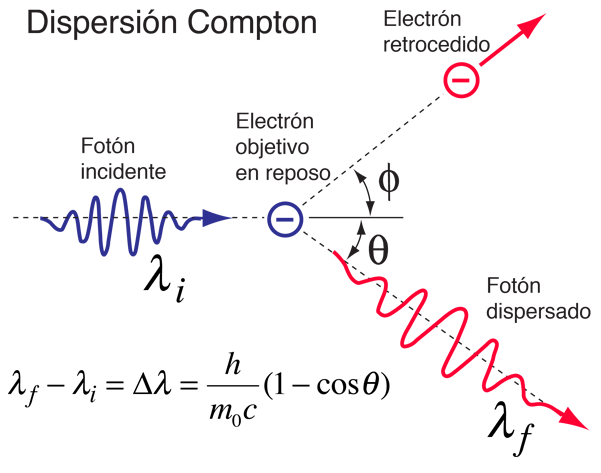
La dispersión de fotones por partículas cargadas se llama dispersión de Compton, en honor a Arthur Compton, que fue el primero en medir la dispersión fotón-electrón en 1922. Cuando el fotón entrante da parte de su energía al electrón, entonces el fotón dispersado tiene una energía más baja, y de acuerdo con la fórmula de Planck, tiene una frecuencia más baja y mayor longitud de onda. El cambio de longitud de onda en tal dispersión para una partícula objetivo dada, sólo depende del ángulo de dispersión. La constante en la fórmula de Compton anterior, se puede escribir

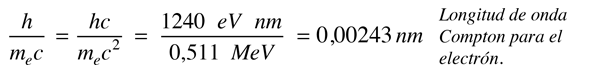
y es denominada longitud de onda Compton del electrón. La fórmula asume que la dispersión ocurre en un marco de electrón en reposo.

Para una longitud de onda entrante

= nm = x 10^ m

dispersado un ángulo de θ=grados

el cambio en longitud de onda es

= nm = x 10^ m

y la longitud de onda final es

= nm = x 10^ m

Expresado en términos de energía de fotón, la energía del fotón entrante es

= x 10^ eV = x 10^ julios

=eV = keV = MeV

y la energía del fotón dispersado es

= x 10^ eV = x 10^ joules

=eV = keV = MeV

Esto implica que la energía transferida al electrón es

= x 10^ eV = x 10^ julios

=eV = keV = MeV .

Esta exploración está diseñada para aceptar valores en la longitud de onda de entrada, o la energía y el ángulo de dispersión. Los parámetros sin especificar, tomarán los valores del caso de la dispersión de rayos X K-alfa del molibdeno en 90 grados, uno de los resultados históricos de Compton. Se pueden cambiar cualquiera de estos valores de entrada.