Velocidad vs Altura para Lanzamiento Vertical con Arrastre Cuadrático
Se presumirá que un objeto experimenta una fuerza de resistencia del aire proporcional al cuadrado de su velocidad. Si se lanza con velocidad v0 tanto la gravedad como la fuerza de fricción actúan hacia abajo mientras el objeto viaja hacia arriba. La dirección hacia arriba se tomará como positiva, y la velocidad en función de la altura y, es el objeto del cálculo. Las expresiones se desarrollarán para las dos formas de resistencia del aire que se utilizarán para las trayectorias:
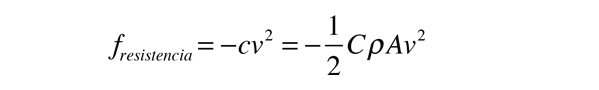
aunque los primeros pasos se realizarán solo con la forma -cv2 por simplicidad.
La ecuación diferencial para el movimiento es
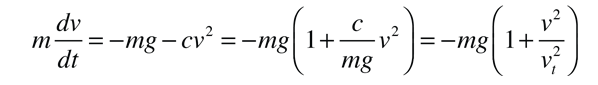
que expresa la fuerza en términos de la velocidad terminal vt:
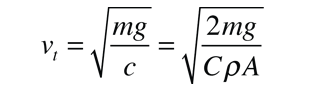
La ecuación de movimiento se puede convertir en una en la que la variable independiente sea la distancia en lugar del tiempo, haciendo uso de la expresión
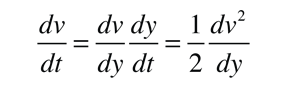
Esto se puede usar para reescribir la ecuación del movimiento anterior como
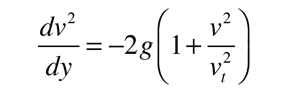
y haciendo la sustitución
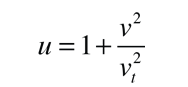
la ecuación de movimiento se puede escribir
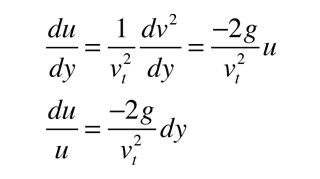
Esta ecuación ahora se puede integrar para dar
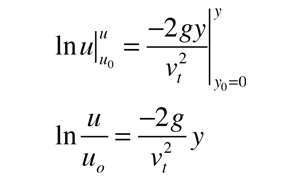
Ahora sustituyendo por u y con varios pasos de reordenamiento algebraico
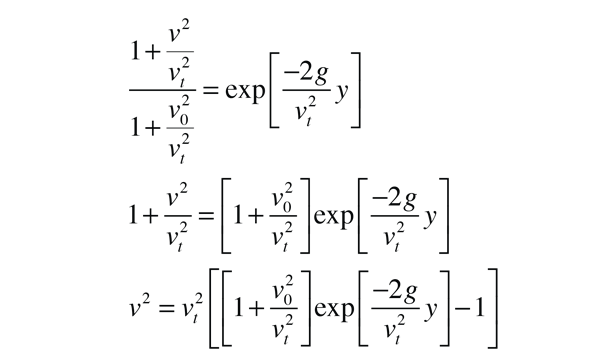
llegamos finalmente a una expresión para la velocidad ascendente en función de la altura:
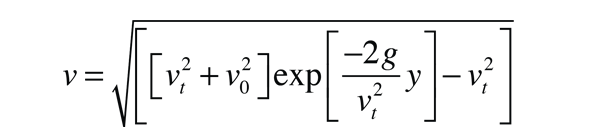
Esta expresión solo se aplica a la parte ascendente del movimiento, ya que la velocidad se vuelve cero en ese punto, y al comenzar su movimiento descendente, la fuerza de arrastre se invierte en dirección. Para esa parte del movimiento, vea el desarrollo de caída libre.
Esta expresión se usa en el cálculo de la trayectoria vertical.
Fricción de Fluidos
Referencia
Fowles & Cassiday
Sec. 2.4
| HyperPhysics*****Mecánica*****Fluidos | M Olmo R Nave |