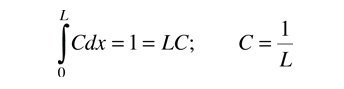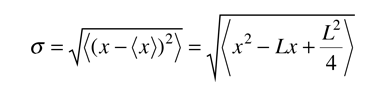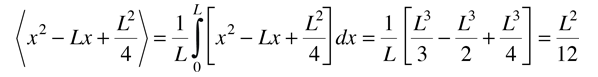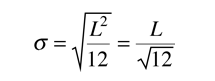La Desviación Típica
La desviación de la raiz cuadrada de la media de x (valor esperado), de su promedio, se llama desviación típica. En un conjunto de medidas discretas, la desviación típica toma la forma
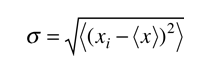 | para medidas discretas de x |
y
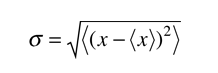 | para un continuo x donde < > implica promedio. |
Para determinar el promedio o el valor esperado (media) en la expresión de arriba, tenemos que hacer uso de la siguiente función de distribución de la variable
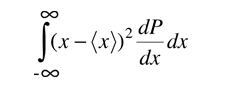
| Ejemplo de Partícula Libre en una Caja |
Conceptos de Estadística Aplicada
| HyperPhysics*****HyperMath*****Álgebra | M Olmo R Nave |