Ecuación de Estado de Van der Waals
La ley de gas ideal trata a las moléculas de un gas, como partículas puntuales con colisiones perfectamente elásticas. Esto funciona bien en muchas circunstancias experimentales, con gases diluidos. Pero las moléculas de gas no son masas puntuales, y hay circunstancias donde las propiedades de las moléculas, tienen un efecto medible experimentalmente. Johannes D. van der Waals en 1873 propuso una modificación de la ley de gas ideal, para tener en cuenta el tamaño molecular y las fuerzas de interacción moleculares. Se la refiere normalmente como la ecuación de estado de van der Waals.
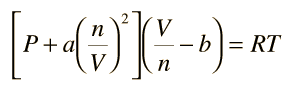
Las constantes a y b tiene valores positivos y son características del gas individual. La ecuación de estado de van der Waals, se aproxima a la ley de gas ideal PV=nRT a medida que el valor de estas constantes se acercan a cero. La constante a provee una corrección para las fuerzas intermoleculares. La constante b es una corrección para el tamaño molecular finito y su valor es el volumen de una mol de átomos o moléculas.
| Helio | ||
| Neón | ||
| Hidrógeno | ||
| Dióxido de Carbono | ||
| Vapor de agua | ||
Puesto que la constante b es indicativa del volumen molecular, se podría usar para la estimación del radio de un átomo o molécula modelado como una esfera. Fishbane et al. da el valor de b para el gas nitrógeno como 39,4 x 10-6 m3/mol. Esto nos lleva a la siguiente estimación del radio:
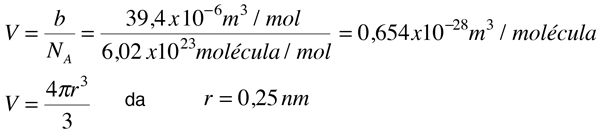
En la tabla periódica se encuentra un radio atómico de 0,075 nm. para el nitrógeno, de modo que es creible la estimación de arriba para la molécula de nitrógeno.
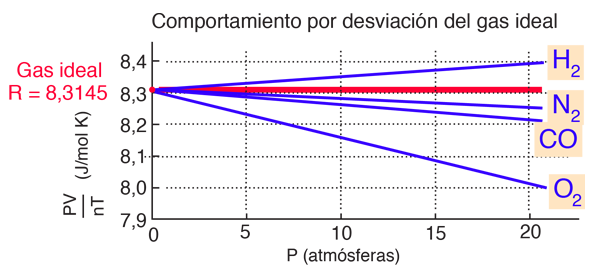
La gráfica de abajo (por Fishbane, et al.) muestra la diferencia significativa con la ley de gas ideal, un 3% en 20 atmósferas de presión para el oxígeno. La desviación es medible incluso a una atmósfera de presión, pero no es grande. El hecho de que todos los gases se extrapolen al mismo valor, es la base para la definición de la escala de temperaturas Kelvin en función de ese valor límite.
Conceptos sobre la Ley de Gas
Conceptos sobre Teoría Cinética
Referencia
Fishbane, Gasiorowicz, Thorton
Sec. 19-3
| HyperPhysics*****Termodinámica | M Olmo R Nave |