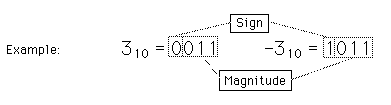
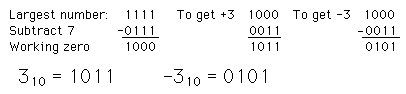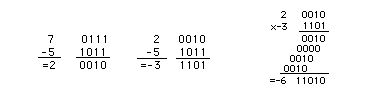Representaciones de Enteros con Signo

Magnitud con signo: al bit mas significativo se le asigna el signo algebráico.

Binario Offset: se resta su mitad al número mas grande posible, para obtener el valor que representa. Es decir se utiliza la mitad del número mas grande posible para representar el "cero" de la escala. Para cuatro bits:

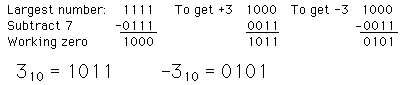
Complemento a 2: los enteros negativos son el complemento del entero positivo mas uno.

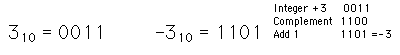
Otras Representaciones de Enteros

Decimal Codificado Binario (BCD o 8421 BCD): cada dígito individual del número decimal, se representa por un número binario de 4 bits.

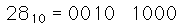
Exceso-3: sumar 3 al número, luego representarlo por un número binario de 4 bits.

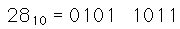
Código 4221: lo cuatro bits representan 4,2,2,1 en vez de 8,4,2,1

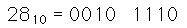
Código Gray: Empezando en cero, hacer un cambio en el bit menos significativo para pasar al siguiente dígito

Representación de "Magnitud con Signo"

El bit mas significativo de un número binario se puede utilizar para representar el signo del número, usando los otros bits para representar su magnitud. Es una forma natural de representación de los enteros con signo, pero no es muy usada porque es incómodo en la aritmética, en comparación con otros sistemas como el complemento a 2. Tambien hay dos ceros, puesto que +0 y -0, tienen códigos diferentes.

Representación Binaria Offset

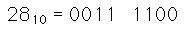
Una forma lógica de representar los enteros con signo es teniendo suficiente rango de números binarios, de modo que el cero pueda establecerse en mitad del rango de los números binarios positivos. Entonces, la magnitud de un número binario negativo se puede obtener restándolo simplemente de ese punto cero. Este sistema tiene la ventaja de una progresión binaria simple desde números negativos hasta positivos. Es útil en contadores binarios y en la conversión de A/D y D/A. Tiene la incomodidad en la computación, en comparación con el sistema de representacion de complemento a 2.

Como un simple ejemplo, considérese un número binario de 4 bits que tiene un máximo de 15. Restándole 7 da la siguiente representación:

Representación de Complemento a 2

En la computación de enteros este código es el mas ampliamente usado. Los números positivos se representan por números binarios sin signo. Los números negativos se forman con el siguiente procedimiento.

Para representar el número -5:

Este código tiene la ventaja de que las operaciones aritméticas son directas. La resta se logra con la suma binaria del complemento a 2. Tambien se puede llevar a cabo la multiplicación.