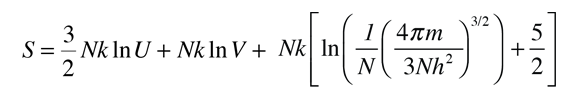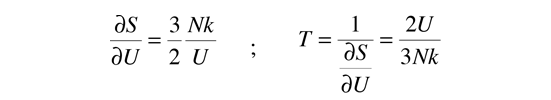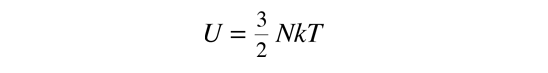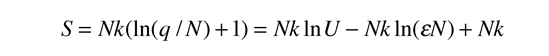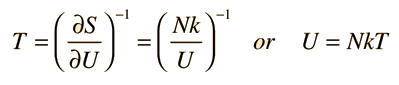A More General View of Temperature
When a high temperature object is placed in contact with a low temperature object, then energy will flow from the high temperature object to the lower temperature object, and they will approach an equilibrium temperature. When the details of this common-sense scenario are examined, it becomes evident that the simple view of temperature embodied in the commonly used kinetic temperature approach has some significant problems.
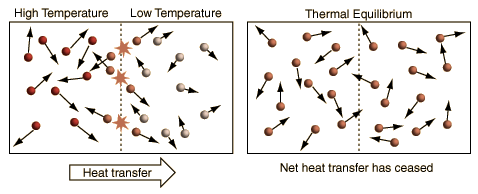
The above illustration summarizes the situation when the kinetic temperature gives a reasonable general description of the nature of temperature. For monoatomic gases acting like point masses, a higher temperature simply implies higher average kinetic energy. Faster molecules striking slower ones at the boundary in elastic collisions will increase the velocity of the slower ones and decrease the velocity of the faster ones, transferring energy from the higher temperature to the lower temperature region. With time, the molecules in the two regions approach the same average kinetic energy (same temperature) and in this condition of thermal equilibrium there is no longer any net transfer of energy from one object to the other.
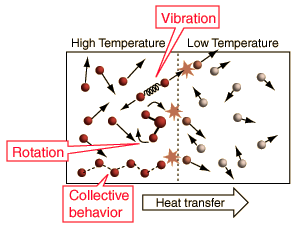 |
The concept of temperature is complicated by internal degrees of freedom like molecular rotation and vibration and by the existence of internal interactions in solid materials which can include collective modes. The internal motions of molecules affect the specific heats of gases, with diatomic hydrogen being the classic case. Collective modes affect the specific heats of solids, particularly at low temperatures. |
Complications such as these have led to the adoption of a different approach to the concept of temperature in the study of thermodynamics. Schroeder's proposal for a theoretical definition of temperature is:
- "Temperature is a measure of the tendency of an object to spontaneously give up energy to its surroundings. When two objects are in thermal contact, the one that tends to spontaneously lose energy is at the higher temperature." (Thermal Physics, Ch 1.)
The kinetic temperature for monoatomic ideal gases described above is consistent with this definition of temperature for the simple systems to which it applies. In that case the equilibrium reached is one of maximum entropy, and the rate of approach to that state will be proportional to the difference in temperature between the two parts of the system. Noting that the equilibrium state of a collection of particles will be the state of greatest multiplicity, then one can define the temperature in terms of that multiplicity (entropy) as follows:
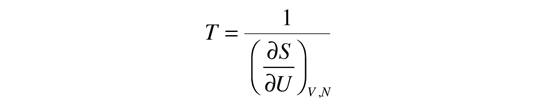
Temperature is expressed as the inverse of the rate of change of entropy with internal energy, with volume V and number of particles N held constant. This is certainly not as intuitive as molecular kinetic energy, but in thermodynamic applications it is more reliable and more general.
| Temperature in terms of entropy |
Temperature concepts
Reference
Schroeder
Ch 1,3
| HyperPhysics***** Thermodynamics | R Nave |