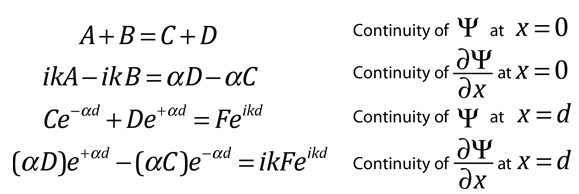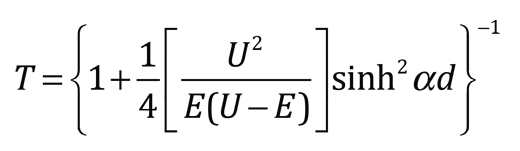Barrier Penetration

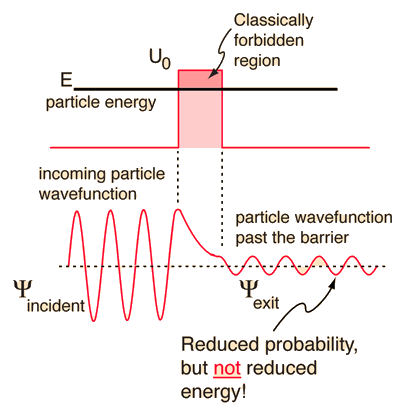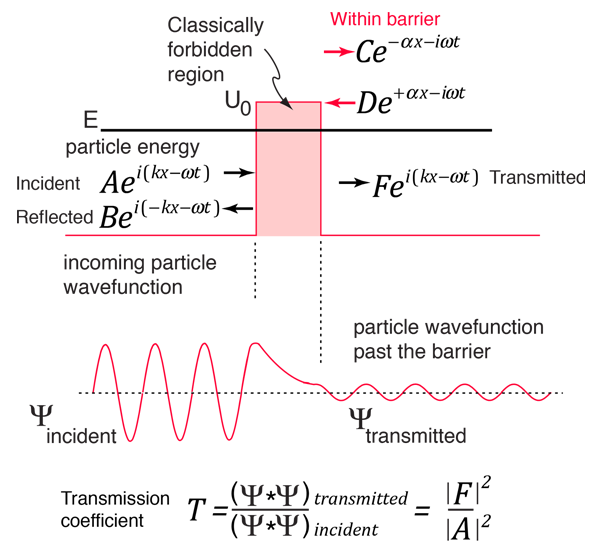
According to classical physics, a particle of energy E less than the height U0 of a barrier could not penetrate - the region inside the barrier is classically forbidden. But the wavefunction associated with a free particle must be continuous at the barrier and will show an exponential decay inside the barrier. The wavefunction must also be continuous on the far side of the barrier, so there is a finite probability that the particle will tunnel through the barrier.

As a particle approaches the barrier, it is described by a free particle wavefunction. When it reaches the barrier, it must satisfy the Schrodinger equation in the form

which has the solution

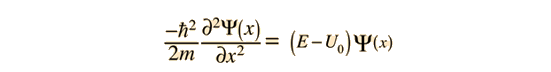
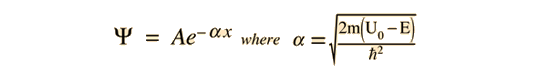
Note that in addition to the mass and energy of the particle, there is a dependence on the fundamental physical constant Planck's constant h. Planck's constant appears in the Planck hypothesis where it scales the quantum energy of photons, and it appears in atomic energy levels which are calculated using the Schrodinger equation.

There are circumstances where a reasonable approximation of the transmission coefficient through the barrier may be obtained by just taking the square of the ratio of the amplitudes of the wavefunctions at the exit and entrance to the barrier. That approximation to the transmission coefficient can be expressed as:

This approximation will be evaluated below and compared to a more rigorous quantum mechanical treatment.

If a particle of energy E =x10^ joules = eV =MeV =GeV

and mass

m = x 10^ kg = me = mp = MeV/c2,

approaches a barrier of height

U0 = x 10^ joule = eV= MeV,

and thickness

d = x 10^ m = nm= fermi,

then the attenuation factor is

α = x10^ 1/m .

and the ratio of the exit and incident amplitudes is x10^ .

Since the probability is proportional to the square of the amplitude, the approximate tunneling probability is T = x10^ .

This approximate approach to the transmission coefficient through the barrier was used in the introduction to alpha decay, which proceeds by quantum mechanical tunneling through the Coulomb barrier, and was used to approximate the decay half-life of Polonium.

The accuracy of this approximate approach is not sufficient for tunneling applications in solid state electronics, where one may deal with the tunneling of electron flow through very thin insulating layers. The more rigorous treatment of the transmission coefficient gives the expression

Using the more rigorous requirement of continuity of both the wavefunction and its first derivative at both boundaries, the transmission coefficient for the barrier described above becomes T = x10^ .

Alpha decay barrier
Details about the transmission coefficient calculation
 Index

Schrodinger equation concepts

Beiser
Concepts of Modern Physics,
Ch 5
 
HyperPhysics***** Quantum Physics R Nave
 Go Back





Quantum Mechanical Barrier Penetration

According to classical physics, a particle of energy E less than the height U0 of a barrier could not penetrate - the region inside the barrier is classically forbidden. But the wavefunction associated with a free particle must be continuous at the barrier and will show an exponential decay inside the barrier. The wavefunction must also be continuous on the far side of the barrier, so there is a finite probability that the particle will tunnel through the barrier. In addition to being continuous at the entrance and exit from the barrier, the first derivative of the wavefunction must also be continuous upon entrance and exit from the barrier. Since the probability of detecting the particle is proportional to the square of the wavefunction, the transmission coefficient through the barrier is proportional to the square of the transmitted wavefunction divided by the square of the incident wavefunction. But since the wavefunction can reflect from the first and second surfaces of the barrier, deriving the expression for the transmission coefficient is a non-trivial mathematical exercise.

Solving for the transmission coefficient requires evaluation of the boundary conditions at the barrier surface.

The equations can be divided through by A since it sets the scale for the other amplitudes. That gives four equations with four unknowns which can be solved by repeated substitutions. The resulting single equation for the transmission coefficient can be expressed in terms of the known parameters of the barrier.

The transmission coefficient can be calculated in the Javascript calculation above.

Alpha decay barrier
 Index

Schrodinger equation concepts

Beiser
Concepts of Modern Physics,
Ch 5

Serway, Moses, Moyer
Modern Physics, 2nd Ed
Ch 6
 
HyperPhysics***** Quantum Physics R Nave
 Go Back