Lagrange Points of the Earth-Sun System

A mechanical system with three objects, say the Earth, Moon and Sun, constitutes a three-body problem. The three-body problem is famous in both mathematics and physics circles, and mathematicians in the 1950s finally managed an elegant proof that it is impossible to solve. However, approximate solutions can be very useful, particularly when the masses of the three objects differ greatly.

18th century mathematicians Leonhard Euler and Joseph-Louis Lagrange discovered that there were five special points in this rotating reference frame where a gravitational equilibrium could be maintained. These five points were named Lagrange points and numbered from L1 to L5. That is, an object placed at any one of these five points in the rotating frame would stay there, with the effective forces with respect to this frame canceling. The Lagrange points can be visualized as three-body equipotential surfaces. Objects placed at the LaGrange points of the Earth-Moon system could be maintained there and would then orbit the Sun, keeping the same relative position with respect to the Earth-Moon system.

In recent years a number of space exploration satellites have made use of the Earth-Sun Lagrange points for positioning observational satellites. The diagram below gives the general geometry, but the great mass difference between the Sun and the Earth makes it hard to draw the Earth-Sun Lagrange points to scale. While L3 would be on the opposite side of the Sun and therefore not obviously useful, Lagrange points L1 and L2 have been used for observational satellites.

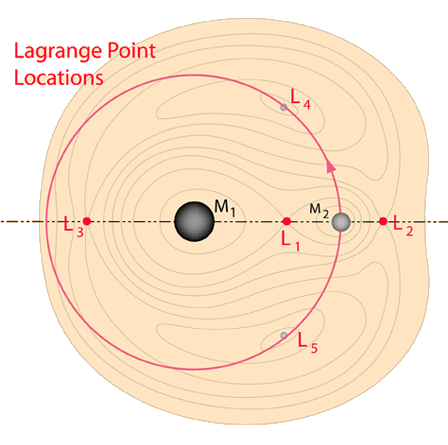The Lagrange points L4 and L5 constitute stable equilibrium points, so that an object placed there would be in a stable orbit with respect to M1 and M2. With small departures from L4 or L5, there would be an effective restoring force to bring a satellite back to the stable point.

The Lagrange points L1, L2 and L3 would not appear to be so useful because they are unstable equilibrium points. Like balancing a pencil on its point, keeping a satellite there is theoretically possible, but any perturbing influence will drive it out of equilibrium. However, in practice these Lagrange points have proven to be very useful indeed since a spacecraft can be made to execute a small orbit about one of these Lagrange points with a very small expenditure of energy. They have provided useful places to "park" a spacecraft for observations. These orbits around L1 and L2 are often called "halo orbits".

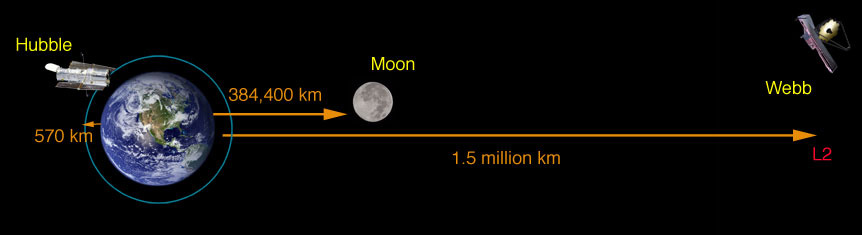
The Earth-Sun Lagrange point L2 has been used for the Wilkinson Microwave Anisotropy Probe (WMAP). L2 is positioned outside the Earth's orbit so that the WMAP can always face away from both the Sun and the Earth, an important feature of a deep-space probe so that it can employ ultra-sensitive detectors without the danger of them being "blinded" by looking at the Sun or the Earth.

This L2 point was also used for the Planck satellite for the study of the Cosmic Microwave Background, and will be used for the James Webb Space Telescope.

The Earth-Sun L2 Lagrange point is outward from the Earth about 1% of the Earth-Sun distance.

NASA Images

References:

Lagrange Point wiki

WMAP at Lagrange point L2

Joseph Louis Lagrange

Lagrange was and 18th century mathematician who tackled the famous "three-body problem" in the late 1700s. The problem cannot be solved exactly, but he found that in the case where the third body is very small compared to the other two, some useful approximate solutions could be found.