Multiplicity for Energy Distribution

The evaluation of the number of ways you can distribute energy among a collection of particles or systems is important in physical calculations since any collection will tend toward the configuration of maximum multiplicity (maximum entropy).

The multiplicity Ω for q units of energy among N equally probable states is given by the expression:

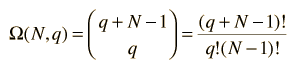
This is sometimes called the number of microstates for the system.

Shroeder has a succinct way to demonstrate the above relationship. Suppose we use a dot to represent each of the q units of energy and a vertical line to denote the boundaries between the N states. An example of a distribution of q=8 units of energy in N=4 states would be

Now this can be seen as a distribution of two types of items, energy units and state boundaries. There would always be q units of energy and N-1 state boundaries for a total of q + N - 1 symbols. So the number of ways to distribute q units of energy would just be the combination

which is the number of ways you can pick q units of energy (the permutation) divided by the the number of ways to rearrange the q units of energy without changing the number in each state.