Law of Sines
The law of sines is used to find angles of a general triangle. If two sides and the enclosed angle are known, it can be used in conjunction with the law of cosines to find the third side and the other two angles.
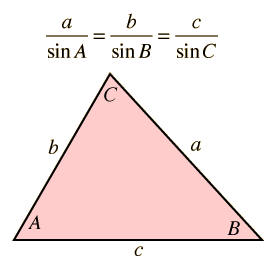 | If two sides and the angle opposite one of them are specified, then the angle opposite the other can be calculated. The third angle is then determined by the fact that the sum of the interior angles of a triangle must equal to 180 degrees. |
Applications
| HyperPhysics*****HyperMath*****Trigonometry | R Nave |