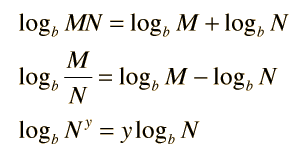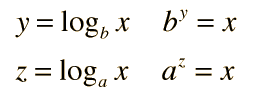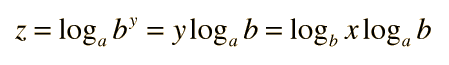Types of Logaritms
Although a logarithm may be defined with any base, the logs most often encountered are the logarithm to the base 10 which is called the common logarithm
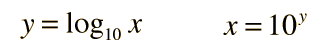
and the logarithm to the base e which is called the natural logarithm.
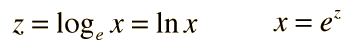
Base changes can be accomplished. For a chosen base:
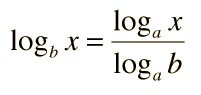
Logarithms may be manipulated with the combination rules.
| HyperPhysics*****HyperMath*****Logarithms | R Nave |
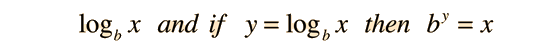 .
.