Henry's Law

When a gas is in contact with the surface of a liquid, the amount of the gas which will go into solution is proportional to the partial pressure of that gas. A simple rationale for Henry's law is that if the partial pressure of a gas is twice as high, then on the average twice as many molecules will hit the liquid surface in a given time interval, and on the average twice as many will be captured and go into solution. For a gas mixture, Henry's law helps to predict the amount of each gas which will go into solution, but different gases have different solubilities and this also affects the rate. The constant of proportionality in Henry's law must take this into account. For example, in the gas exchange processes in respiration, the solubility of carbon dioxide is about 22 times that of oxygen when they are in contact with the plasma of the human body.

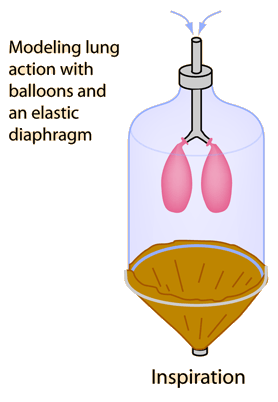
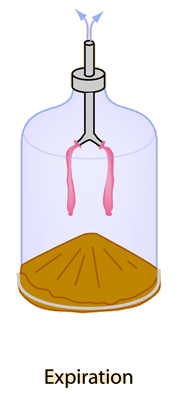
Graham's Law

When gases are dissolved in liquids, the relative rate of diffusion of a given gas is proportional to its solubility in the liquid and inversely proportional to the square root of its molecular mass. Important in the transport of respiration gases is the relative diffusion rate of oxygen and carbon dioxide in the plasma of the human body. Carbon dioxide has 22 times the solubility, but is more massive (44 amu compared to 32 for oxygen). According to Graham's law, the relative rate of diffusion is given by

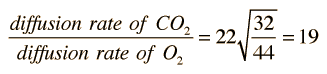
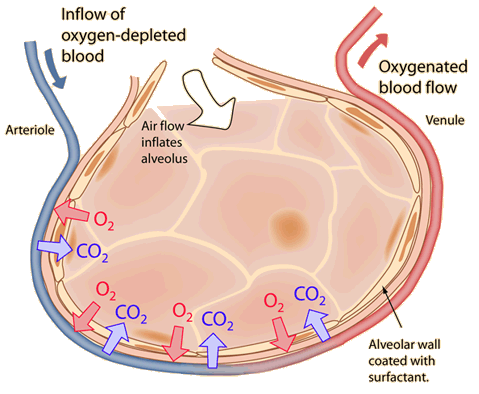Graham's law may be applied to the process that occurs in the alveoli of the lungs.

Fick's Law

The net diffusion rate of a gas across a fluid membrane is proportional to the difference in partial pressure, proportional to the area of the membrane and inversely proportional to the thickness of the membrane. Combined with the diffusion rate determined from Graham's law, this law provides the means for calculating exchange rates of gases across membranes. The total membrane surface area in the lungs (alveoli ) may be on the order of 100 square meters and have a thickness of less than a millionth of a meter, so it is a very effective gas exchange interface.

Oxygen Transport in the Lungs

The total membrane surface area in the lungs (alveoli ) may be on the order of 100 square meters and have a thickness of less than a millionth of a meter, so it is a very effective gas exchange interface. The relative rate of oxygen and carbon dioxide exchange across these thin membranes depends upon diffusion and the solubility of the gases in the fluid membrane. This is described by Fick's law.

Respiration

The process of respiration involves the lowering of the diaphragm to increase the volume of the thoracic cavity, which by the ideal gas law is seen to lower its pressure. A model of lung action can be made with a bell jar, balloons, and an elastic membrane. The thoracic cavity normally has a negative gauge pressure to keep the lungs inflated, and the diaphragm action must lower it more to accomplish inhalation. The inhalation process must accomplish the inflation of the alveoli of the lungs, which itself is a remarkable process. The pressure achieved by the diaphragm action is only about -4 mmHg compared to a pressure inside the alveoli of about -3 mmHg, so inhalation must be accomplished with a pressure differential of only about 1 mmHg. The remarkable efficiency of oxygen transport across the lung membranes is characterized in Fick's Law.

Breathing Pressure Model

Air is drawn into the lungs by lowering the diaphragm, making the pressure more negative in the thoracic cavity. Exhalation is accomplished by the elastic recoil of the diaphragm and of the tiny air sacs (alveoli ) of the lungs. That elastic recoil produces a positive pressure.