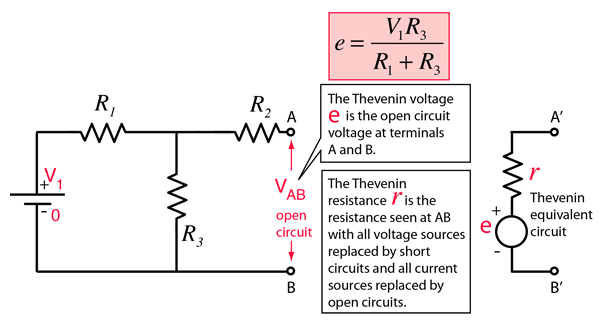
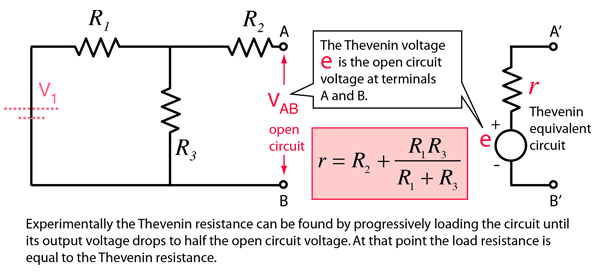
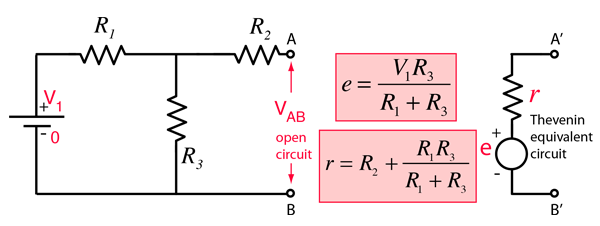
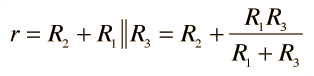Thevenin's Theorem

Any combination of batteries and resistances with two terminals can be replaced by a single voltage source e and a single series resistor r. The value of e is the open circuit voltage at the terminals, and the value of r is e divided by the current with the terminals short circuited.

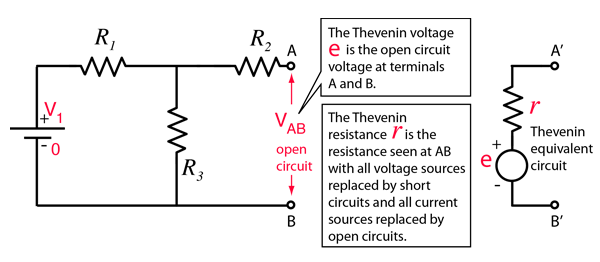
Thevenin Voltage

The Thevenin voltage e used in Thevenin's Theorem is an ideal voltage source equal to the open circuit voltage at the terminals. In the example below, the resistance R₂ does not affect this voltage and the resistances R₁ and R₃ form a voltage divider, giving

Thevenin/Norton Resistance

Thevenin Example

Replacing a network by its Thevenin equivalent can simplify the analysis of a complex circuit. In this example, the Thevenin voltage is just the output of the voltage divider formed by R₁ and R₃. The Thevenin resistance is the resistance looking back from AB with V₁ replaced by a short circuit.

For R1 =Ω, R2

= Ω, R3 =Ω,

and voltage V1 = V

the Thevenin voltage is

V

since R1 and R3 form a simple voltage divider.

The Thevenin resistance is

= Ω.