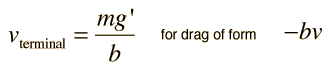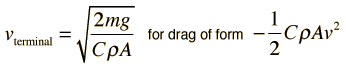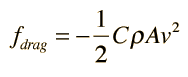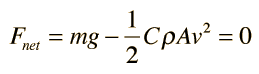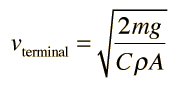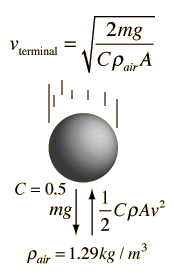Terminal Velocity

When an object which is falling under the influence of gravity or subject to some other constant driving force is subject to a resistance or drag force which increases with velocity, it will ultimately reach a maximum velocity where the drag force equals the driving force. This final, constant velocity of motion is called a "terminal velocity", a terminology made popular by skydivers. For objects moving through a fluid at low speeds so that turbulence is not a major factor, the terminal velocity is determined by viscous drag. The expression for the terminal velocity is of the form
Motion analysis
Objects moving at high speeds through air encounter air drag proportional to the square of the velocity. This quadratic drag leads to a terminal velocity of the form
Examples
 Index

Fluid friction
 
HyperPhysics***** Mechanics ***** Fluids R Nave
 Go Back





Quadratic Velocity Dependence

For large objects moving through air, the air resistance is approximately proportional to the square of the velocity. The form of the resistance is

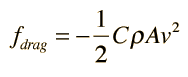
where ρ is the air density, A the crosssectional area, and C is a numerical drag coefficient. The drag coefficient C is 0.5 for a spherical object and can reach 2 for irregularly shaped objects according to Serway. An object falling through the air will reach a terminal velocity when the drag force is equal to the weight:

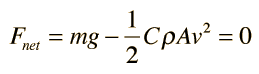
This gives a terminal velocity

Examples
Vertical trajectory with quadratic drag
Freefall velocity with quadratic drag
Freefall velocity with quadratic drag for given fall distance
Freefall velocity with quadratic drag as function of time
Time to peak with quadratic drag
Peak height with quadratic drag
Upward velocity vs height
Fall velocity vs height
Impact velocity
 Index

Fluid friction

Reference
Serwary & Beichner
Ch 6
 
HyperPhysics***** Mechanics ***** Fluids R Nave
 Go Back





Terminal Velocity Examples

Falling objectMass AreaTerminal velocity
Skydiver75 kg 0.7 m260 m/s134 mi/hr
Baseball (3.66cm radius) 145 gm 42 cm2 33 m/s 74 mi/hr
Golf ball (2.1 cm radius) 46 gm 14 cm2 32 m/s 72 mi/hr
Hail stone (0.5 cm radius) .48 gm .79 cm2 14 m/s 31 mi/hr
Raindrop (0.2 cm radius) .034 gm .13 cm2 9 m/s 20 mi/hr


Data from Serway, Physics for Scientists and Engineers, Table 6.1. A drag coefficient C=0.5 is assumed, falling through air.

Hailstone calculation

Calculation for a sphere

 Index

Fluid friction
 
HyperPhysics***** Mechanics ***** Fluids R Nave
 Go Back





Hailstone Terminal Velocity

Contributing to the danger of large hailstones is the fact that they fall faster than small ones. That is, the terminal velocity increases with the size of the hailstone. Assuming the hailstones to be spherical and using a drag coefficient of C = 0.5 gives the following :

Radius (cm)v (km/hr) v(m/s)v(mi/hr)
.0171.94.3
0.122 6.113.7
0.2 318.6 19.3
0.5 49 13.630.5
1.0 69.519.343.2
2.0 98.3 27.3 61
3.0 120 33.4 74.8
5.0 155 43.296.6
10.0 220 61136

General examples

Calculation for a sphere



 Index

Fluid friction
 
HyperPhysics***** Mechanics ***** Fluids R Nave
 Go Back





Terminal Velocity Calculation

For a spherical object falling through air, the terminal velocity for the case of quadratic drag can be calculated from

Hailstone calculation

Other examples

For a sphere of radius r = meters = cm

and density ρ = kg/m3 = gm/cm3 ,

the mass is m = kg = gm,

and the terminal velocity is

vterminal = m/s = km/hr = mi/hr.

 Index

Fluid friction concepts
 
HyperPhysics***** Mechanics ***** Fluids R Nave
 Go Back