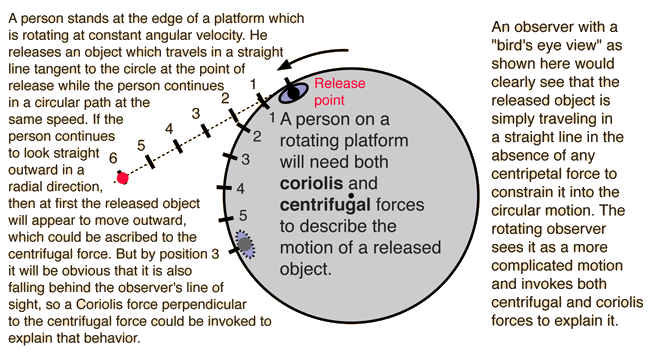
Describing Motion in a Rotating Frame of Reference

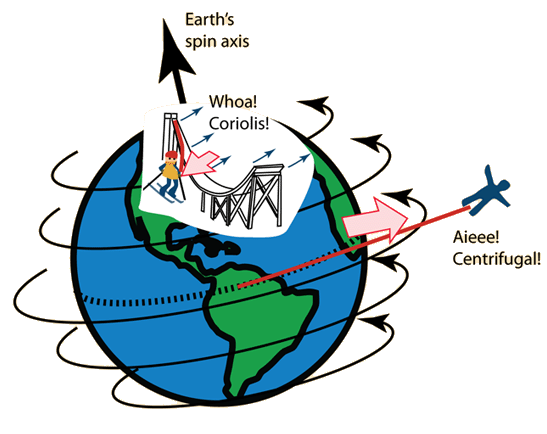If the Earth were spinning much faster, then we would feel the effects of the Earth's rotation much more commonly. The Earth's rotation does have significant influence on the motion of large air masses as in storm systems.

If you are a part of a system that spins or makes high speed turns, as on amusement park rides, you become aware that moving objects in such systems behave differently than normal. We describe these effects of the rotating system in terms of centrifugal force and Coriolis force, both of which might properly be called "effective forces" that we invoke to explain the unique behaviors of objects in such systems.

Newton's second law, F = ma, is used to describe the motion of an object in response to an applied force, but that presumes that the observer is in a non-accelerating reference frame. The term "inertial frame" is commonly used to describe such a frame of reference. If you wish to describe the motion of an object with respect to an accelerating reference frame, then you must transform Newton's second law into that coordinate system, which is not a simple problem.

Example: Centrifugal and Coriolis