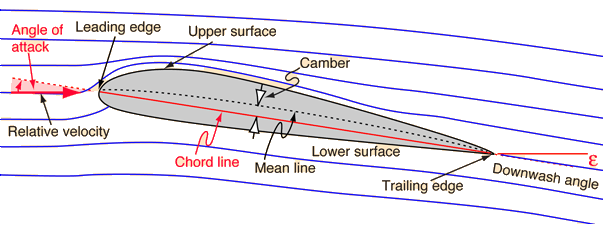
Bernoulli or Newton's Laws for Lift?
Which is best for describing how aircraft get the needed lift to fly? Bernoulli's equation or Newton's laws and conservation of momentum? This has been an extremely active debate among those who love flying and are involved in the field. If the question is "Which is physically correct?" then the answer is clear -- both are correct. Both are based on valid principles of physics. The Bernoulli equation is simply a statement of the principle of conservation of energy in fluids. Conservation of momentum and Newton's 3rd law are equally valid as foundation principles of nature - we do not see them violated. This physical validity will undoubtedly not quell the debate, and this treatment will not settle it. But perhaps it can at least indicate the lines of the discussion.
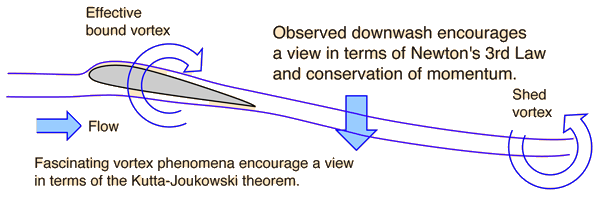
Those who advocate an approach to lift by Newton's laws appeal to the clear existance of a strong downwash behind the wing of an aircraft in flight. The fact that the air is forced downward clearly implies that there will be an upward force on the airfoil as a Newton's 3rd law reaction force. From the conservation of momentum viewpoint, the air is given a downward component of momentum behind the airfoil, and to conserve momentum, something must be given an equal upward momentum. Those who prefer to discuss lift in these terms often invoke the Kutta-Joukowski theorem for lift on a rotating cylinder. The lift on a spinning cylinder has been clearly demonstrated, and its discussion includes a vortex in the circulating air. Many discussions of airfoil lift invoke such a vortex in the effective circulation of air around the moving airfoil. Conservation of angular momentum in the fluid requires an opposite circulation in the air shed from the trailing edge of the wing, and such vortex motion has been observed.
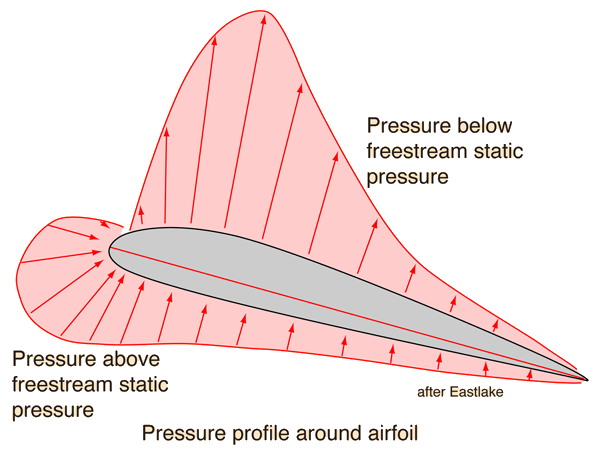
Those who advocate the Bernoulli approach to lift point to detailed measurement of the pressures surrounding airfoils in wind tunnels and in flight. Such pressure measurements are typically done with Pitot tubes. Correlating the pressures with the Bernoulli equation gives reasonable agreement with observations.
Those who argue against modeling the lift process with the Bernoulli equation point to the fact that the flow is not incompressible, and therefore the density changes in the air should be taken into account. This is true -- the ideal gas law should be obeyed and density changes will inevitably result. This does not render the Bernoulli equation invalid, it just makes it harder to apply. But the pragmatic success of modeling the lift with Bernoulli, neglecting density changes, suggests that the density changes are small. Pragmatic difficulties exist also for those who would model the lift from Newton's third law -- it is difficult to measure the downward force associated with the downwash because is is distributed in the airstream leaving the trailing edge of the airfoil. Detractors from the Bernoulli approach often make calculations using the Kutta-Joukowski theorem (see Craig).
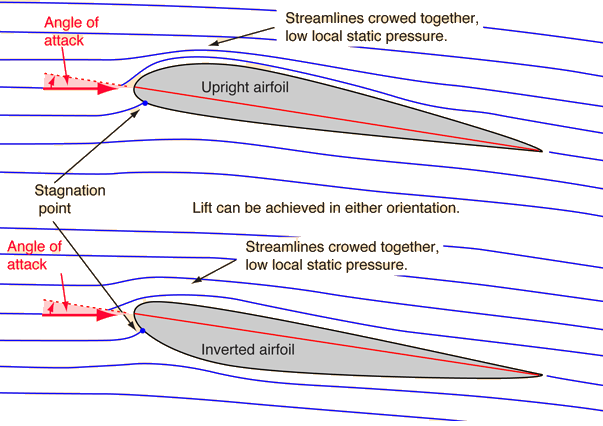
| Illustration of different angles of attack |
Bernoulli concepts
References
Eastlake
Craig

NASA
Aerodynamics
| HyperPhysics***** Mechanics ***** Fluids | R Nave |