Simplified Model: Sound Reinforcement

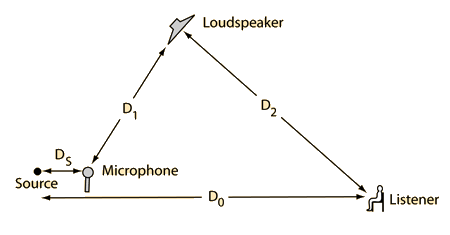
Assume*:

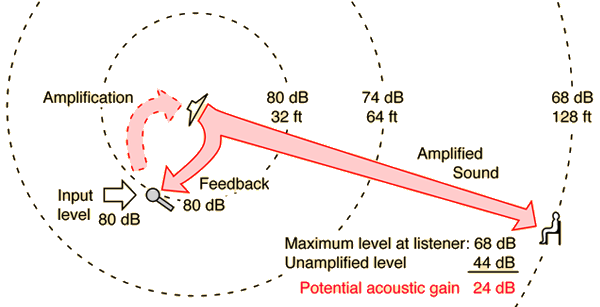
The loudspeaker provides more sound to the listener than would otherwise have been received, but it also produces sound at the location of the microphone. This feedback to the microphone limits the amount of amplification which can be used. Control of the feedback generally is the determining factor for the potential acoustic gain that can be achieved by a sound reinforcement system.
The microphone creates an electrical image of the sound which is amplified and used to drive a loudspeaker.

*These idealizations are never met in any real room, but they provide a framework for building a model. The assumptions will be relaxed later.

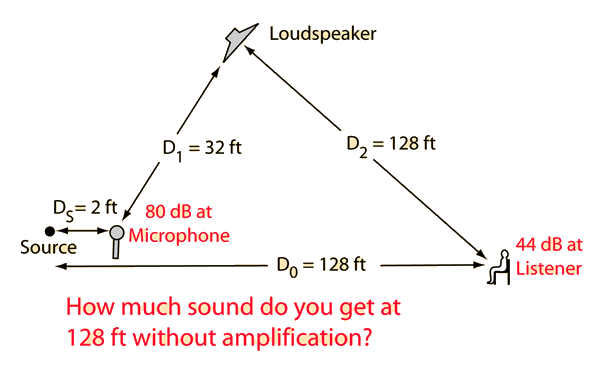
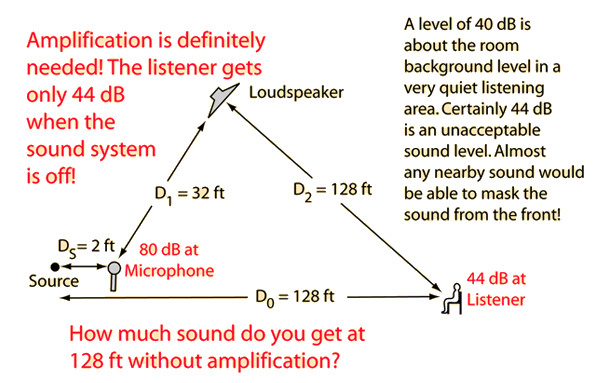
Numerical example
 Index

Sound reproduction concepts
 
HyperPhysics***** Sound R Nave
 Go Back








Numerical Example: Need for Amplification

By the inverse square law, a doubling of distance will drop the sound intensity to 1/4, corresponding to a drop of 6 decibels. Note that in the table at right, the distance is doubled in each successive step.

Simplified sound
system model
Level
dB
Distance
ft
80
2
74
4
68
8
62
16
56
32
50
64
44
128
The following simplifying assumptions allow us to calculate the sound levels and assess the need for amplification:
1. The sound drops off according to the Inverse square law.
2. The microphones and loudspeakers are omnidirectional.
Is this loud enough?How much can you amplify it?
 Index

Sound reproduction concepts
 
HyperPhysics***** Sound R Nave
 Go Back
















Numerical Example: Need for Amplification

Level
dB
Distance
ft
80
2
74
4
68
8
62
16
56
32
50
64
44
128
Starting with 80 dB at two feet and using the fact that every doubling of distance will drop the level by 6 dB, we learn that a listener at 128 ft would receive a sound intensity of only 44 dB!
How much can you amplify it?
 Index

Sound reproduction concepts
 
HyperPhysics***** Sound R Nave
 Go Back








Maximum Amplification Condition

When the feedback to the microphone is equal to the original sound input level, the gain can no longer be increased without an uncontrolled increase in output, usually in the form of a loud ring at one frequency. Practically, the sound should be kept about 3 dB below that point. If 80 dB is the input level to the microphone, then 80 dB feedback return is an upper bound. Using the inverse square law, the resulting levels are as shown.

Numerical examplePotential Acoustic Gain
 Index

Sound reproduction concepts
 
HyperPhysics***** Sound R Nave
 Go Back