Digital Sampling
For the purpose of storing audio information in digital form, like a compact disc, the normal continuous wave audio signal (analog) must be converted to digital form (analog-to-digital) conversion. Below is an example of a D/A conversion using digits 0-9, but practical schemes store the numbers in binary form. The number of bits in the binary sampler determines the accuracy with which the analog signal can be represented in digital form.
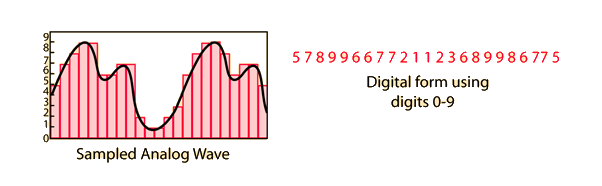
From this crude picture of digitizing in steps, perhaps you can appreciate the industry standard of 16 bit sampling in which the voltage is sampled into 65,536 steps. In addition to the number of steps, the rate of sampling also affects the fidelity of representation of the analog waveform. The standard sampling rate is 44.1 kHz, so the assignment of one of 65, 536 values to the signal is done 44,100 times per second. If this recorded data is read from the CD in real time, you are processing 1.4 million bits of information per second (1.4 Mbps).
| MP3 Digital |
Traveling wave concepts
Sound reproduction concepts
Audio signal concepts
| HyperPhysics***** Sound | R Nave |